Representación, desarrollo y secciones planas.
El Tetraedro se puede considerar como una pirámide recta y regular, de cuatro caras idénticas cuya base y, por tanto, sus caras laterales, son triángulos equiláteros. Los lados de estos triángulos son las aristas de la superficie.
Tetraedro con una de sus caras apoyada en el plano horizontal de proyección.
Dibujamos una de estas caras sobre el plano horizontal de proyección para una magnitud arbitraria de la arista y completamos esta vista dibujando la proyección del vértice superior V que coincide con el centro del triángulo.
Para dibujar la proyección vertical, tendremos en cuenta que la magnitud de la altura del tetraedro está en función de la magnitud de sus aristas. Ésta es el cateto mayor de un triángulo rectángulo, siendo el cateto menor la proyección horizontal de una de las aristas (v-b) y la hipotenusa, la verdadera magnitud de dicha arista.
Tetraedro regular 1.
Tetraedro con una de sus aristas contenida en plano horizontal de proyección siendo otra horizontal.
Cuando el tetraedro está en esta posición, el contorno aparente de sus aristas en proyección horizontal es un cuadrado.
Las
diagonales de este cuadrado son las aristas “contenida y paralela” al
plano horizontal de proyección (a las que se hace referencia en el
título) que están en verdadera magnitud. Dibujaremos
por tanto un cuadrado a partir de sus diagonales de valor igual al valor
constante de la arista del cuerpo. Figura 2
La altura -h- del cuerpo es la mínima distancia existente entre las dos aristas mencionadas o, la distancia entre los puntos medios m y n de ambas. Dicha altura es, a su vez, cateto mayor de un triángulo rectángulo de cateto menor la mitad de la arista del cuerpo e hipotenusa la apotema
(o altura) de una de las caras según se advierte en la ilustración de
la figura 3. Determinada la altura, dibujamos la proyección vertical del
cuerpo.
Tetraedro 2.
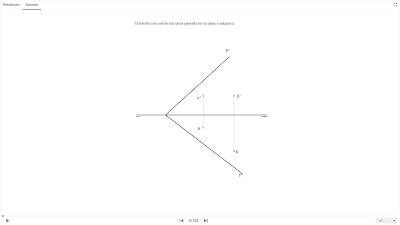
Tetraedro con una de sus caras apoyada en un plano cualquiera.
Dado el plano oblicuo Q, dibujaremos sobre él un tetraedro de arista definida y centro O de dicha cara en él contenida.
Abatimos el centro O dado sobre uno de los planos de proyección, en el ejercicio de la figura 4 sobre el plano horizontal de proyección, y dibujamos en verdadera magnitud, el triángulo equilátero de la cara del tetraedro correspondiente a este centro.
Desabatimos el plano Q y con él la cara ABC dibujada obteniendo de este modo su proyección horizontal.Calculamos la proyección vertical auxiliándonos de rectas del plano (en el ejemplo, horizontales) que contengan a los puntos A. B y C.
El vértice superior V del tetraedro está sobre una recta perpendicular al plano Q que contiene a la base, trazada por el centro O.
Su posición sobre esta perpendicular queda determinada por la altura del tetraedro que, como sabemos, está en función de la arista del cuerpo. Determinamos la altura h sobre la cara abatida como en el ejercicio de la figura 1.
Para situar sobre la recta perpendicular al plano Q, a partir del punto O, la magnitud de la altura, tomamos un punto arbitrario M de esta recta y calculamos la verdadera magnitud del segmento O-M mediante giro. Sobre el segmento o’-M1 (en verdadera magnitud) y a partir de o’, llevamos la altura h determinada y obtenemos el punto V1. Deshaciendo el giro queda determinada la proyección vertical v’ buscada, del vértice superior.
Tetraedro 3.